Matrix Factorization

오늘은 넷플릭스에서 발표한 matrix factorization에 대해서 설명해보려고 합니다.

Matrix Factorization

Matrix Factorization은 User와 Item 간의 정보를 나타내는 User-Item interaction Matrix(Rating Matrix)를 User latent matrix와 Item latent matrix로 분해하는 기법을 말합니다. 이때 Rating Matrix는 (User의 수: N) x (Item의 수: M) 으로 구성된 행렬인데, 각각의 유저가 각각의 아이템에 대한 평가가 수치로 남겨진 행렬이 됩니다. 조금 더 풀어서 설명해볼까요.

1. User-based

또다른 추천 시스템 중 하나인 User-based 추천에 의하면 아래 그림의 joe에게 새로운 영화를 추천해주기 위해서는 joe가 좋아하는 영화들을 동일하게 좋아하는 유저 a, b, c를 찾아서, 그들이 다시 공통적으로 좋아하는 영화를 찾아서 추천을 해주게 됩니다.

그러면 위의 그림과 같이 #1, #2, #3, #4의 영화를 순서대로 추천해줄수 있겠죠

2. Matrix Factorization

그런데 Matrix Factorization은 조금 다른 방법으로 접근합니다. 유저들(User)이 각각의 영화(Item)에 대한 행렬을 분해하면 우리가 알지 못했던 숨겨진 feature가 있다는 것인데요. 아래의 그림을 보시면 아래와 같이 두 개의 축으로 특징들을 분류해볼 수 있습니다.

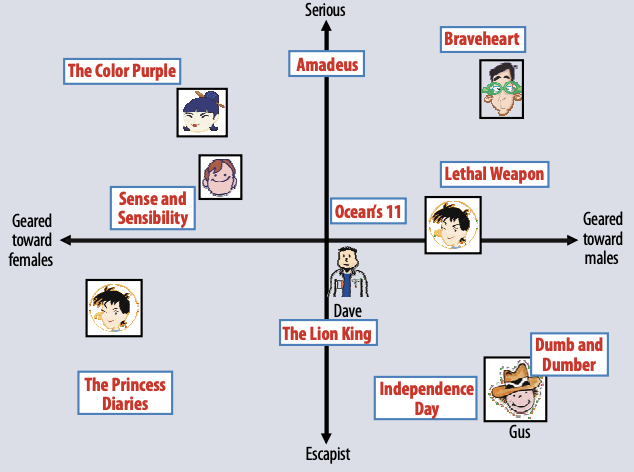
위의 그림에서는 여성과 남성,그리고 현실도피 성향을 가졌는지 진지한 사람인지를 두 축으로 사용하고 있습니다. 처음에 봤던 것처럼 단순히 유사한 것을 찾는 것에 비해서 조금 더 카테고리화 된 것이 보이네요. 이러한 방법은 많은 유저들이 아이템에 대한 평점을 많이 남겨주는 경우에 아주 쉽고 간단하게 사용될 수 있습니다.

하지만 현실적으로 생각해봤을 때, 유저들이 영화에 대해 평점을 많이 남겨주는 경우(일종의 Explicit Feedback)는 드뭅니다. 그러다 보니 Rating Matrix 자체가 sparse한 경우가 많죠. 대신에 이런 Matrix Factorization은 새로운 아이템이 들어오는 경우에 강점을 가질 수 있습니다. 특히나 넷플릭스와 같이 컨텐츠가 끊임없이 추가되는 경우에는 유저에게 새로운 작품에 대한 선호도를 평가하고 추천해줘야 하는데, 이런 알고리즘이 적합하게 쓰일 수 있게 됩니다.

한편 자료에 의하면 유저들의 직접적인 평점 데이터들을 활용하기 어렵다면 Implicit Feedback 을 적용할 수도 있다고 합니다. 대표적으로는 구매 목록이나 브라우저 히스토리, 검색어나 마우스에 의한 이벤트(재생, 멈춤, 나가기 등)들에 대한 기록들로요.

3. Basic Matrix Factorization Model

각 유저의 각 아이템에 대한 평점은 아래와 같이 표기할 수 있습니다.

위와 같이 계산되는 모델은 특잇값 분해로 불리는 SVD와 유사한데, Rating Matrix의 특성 상, 결측치가 많이 발생하므로 SVD를 직접 사용하는 것은 불가능합니다. 그렇다고 해서 결측치를 임의로 사용한다고 하더라도도 과적합 문제가 발생할 수 있으므로 어렵습니다.

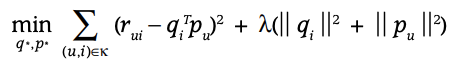
그래서 관측된 값으로만 모델링하는 것이 위와 같이 제안되었는데, 여기에는 과적합을 방지하기 위해 lambda를 통해 제어를 하게 되는데, 이 값은 주로 교차 검증에 의해 결정됩니다.

4. Learning Algorithms

3번의 식을 최소화 하기 위한 방법으로는 두가지 방법을 제시합니다.

4.1 Stochastic Gradient Descent

이 방법으로는 빠르고 쉽게 구현할 수 있는데, 각 training set에 대해 알고리즘은 $r_{ui}$를 예측하고 아래와 같이 오차를 계산할 수 있습니다.

산출한 후에는 gradient 의 반대 방향에서 각 $q_i$와 $p_u$를 아래처럼 수정해서 반영할 수 있습니다.

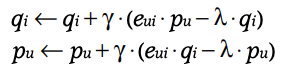
4.2 Alternating Least Squares

위의 식은 $q_{i}$와 $p_{u}$ 둘 다 알 수 없기 때문에 convex하다고 할 수 없습니다. 그래서 이번에는 각각의 값을 고정하면서 최소값을 찾는 방법으로 아래와 같이 동작합니다.

일반적으로는 4.1의 방법이 빠르고 쉽지만 4.2의 방법이 유리할 때도 있는데요, 아래의 경우에 해당합니다.

- 시스템이 병렬화를 지원하는 경우

- 시스템이 Implicit Feedback에 집중되어 있는 경우

5. Additional Input Sources

종종 시스템은 cold start 문제를 해결해야 하는 경우가 있는데, 이는 유저들이 평점 결과를 거의 남기지 않는 상황에 해당한다고 볼 수 있습니다. 이 문제를 해결하기 위한 방법으로는 유저들에 대한 추가적인 정보들을 통합하는 것입니다. 그러니까 행동 정보가 필요하다는 건데, 넷플릭스를 예로 들면 영상을 얼마나 얼마나 오래 유지하면서 보는지, 어떤 방식으로 영상을 보는지에 대한 데이터가 될 수 있습니다.

이와 같이 N(u)에 속한 아이템에 대한 선호를 보인 유저는 아래와 같이 표기합니다.

그런데 이를 정규화하는 것이 일반적으로 더 좋은 결과를 얻을 수 있기 때문에 정규화를 합니다.

또다른 정보는 유저의 속성인데, 인구 통계학적인 정보가 될 수 있습니다. 이를 표현하면 아래와 같습니다.

이를 통하여 모두 통합된 유저의 평점식은 아래와 같이 표현될 수 있습니다.

6. Temporal Dynamics

지금까지의 모델은 사실 정적인 모델인데요. 영화를 포함한 여러 컨텐츠는 시간이 흐르면서 재평가를 받는 경우가 많습니다. 그러므로 User-Item interaction을 좀 더 실시간으로 반영할 수 있는 Temporal Effect에 대해 알 필요가 있습니다.

이는 아래의 세 개의 항을 반영합니다.

- $b_{i}(t) $b_{i} (t)$

- $b_{u}(t)$ 유저의 성향은 시간에 따라 변한다

- $p_{u}(t)$ 아이템에 대한 유저의 선호도는 시간에 따라 변한다

이를 반영하면 식을 아래와 같이 쓸 수 있습니다.

7. Inputs with varying confidence levels

모든 관측값이 같은 신뢰도를 가질 수는 없습니다. 따라서 예측된 값에는 신뢰도가 함께 보여져야 하는데, 이 신뢰도는 행동의 빈도에 따라 숫자로 표현될 수 있습니다. 예를 들면 이 영화를 본 시간이 길수록 신뢰도가 올라갈 수 있는 것이죠. 이를 반영하면 아래와 같은 식을 얻을 수 있습니다.